First a word about numbers in Audulus. All signals in Audulus are stored as 32 bit floating point numbers. This allows Audulus to represent very small and very large values with considerable precision, but it also can lead to unexpected results. Because there is no integer type in Audulus, numbers that appear to be integers are actually floating point numbers i.e. 1 is not really 1 but 1.00000000... Ordinarily this doesn’t cause a problem, but the results of some calculations are necessarily rounded to the number of decimal digits Audulus supports. Because of this, it is good to avoid comparisons for equality when possible. It is much better to write x <= 0 than x == 0. It is also worth noting that the value node does not always display the full internal precision for a number.
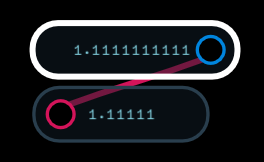
Similarly:
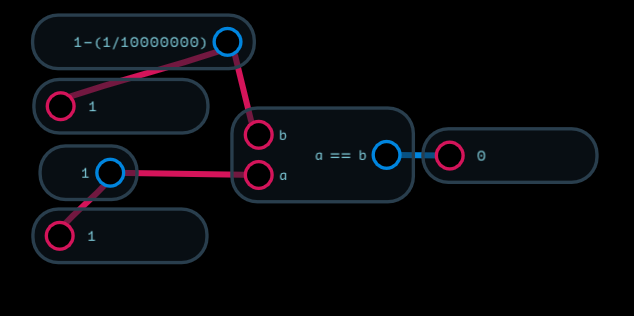
but subtract a little bit less from 1 and you get:
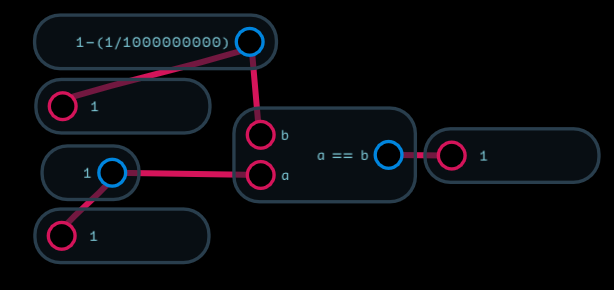
Be careful of rounding errors.
The Expression Node
Audulus provides an expression node which allows you to evaluate a variety of mathematical expressions which can’t be calculated with the add and multiply nodes. The expression node uses a subset of the mathematical operators and functions commonly available in the C programming language. It can have multiple inputs but only has a single output. Each variable used in the expression becomes an input. The expression a + b becomes:
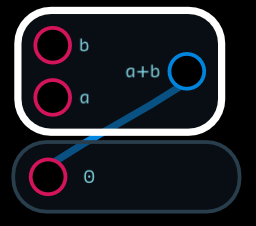
Variable names must start with a letter but can contain numeric digits. Certain names represent constants and function names and are reserved. If the expression you entered cannot be processed because of a syntax error it will display no inputs and output zero. Check for unbalanced parentheses, reserved words used as variables, and functions with an incorrect number of parameters.
Operator Precedence
Consider the following expression: a = b + c * d. In what order will this be evaluated? If we were to go left to right, you would first add b to c, then multiple the result by d and then assign the value to a. What in fact happens is c is multiplied by d then the result is added to b and finally assigned to a.
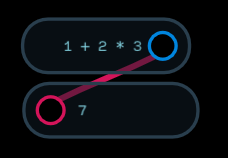
Why does this occur? The operators in the expression node have different priorities and some operations are carried out before others. This is commonly referred to as operator precedence.
The expression node has three classes of operator. Unary operators take a single operand. Audulus has 2 unary operators, + and -. These unary operators are placed before their operand i.e. -3 or +1. The + unary operator is rarely used. Binary operators take 2 operands and are the most common operators in Audulus.
The + and - operators can also be binary operators i.e. 1 + 2 or 3 - 2. In addition we have * / ^ and the comparison operators. Because there is no integer or boolean type available in Audulus there are also no operators of these types. There is one tertiary operator in Audulus, the ? operator. The order in which these operators are evaluated is as follows. Within each group operators are evaluated in left to right order.
Parentheses
() - parentheses are used to group expressions and control the order of evaluation. The expression within the innermost set of parentheses is evaluated first, then then next outward set, etc.
Unary operators
+ -
Binary operators
exponentiation ^
multiplication and division * /
addition and subtraction + -
comparison operators < > <= >= != ==
Tertiary operator
conditional operator ?
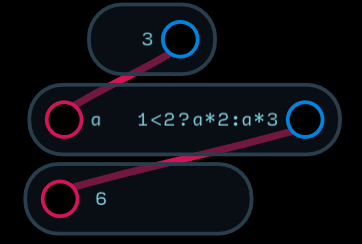
The conditional operator takes 3 operands with the last 2 separated by a : i.e a ? b : c. The a operand is evaluated first. If it is greater than 0, the b operand is evaluated and becomes the result. If a evaluates to less than or equal to zero, the c operand is evaluated and becomes the result of the expression. For example:
Parentheses can be used to group multiple ? expressions. I find it easier to place the next ? expression at the end of the first one i.e.
a ? b : (c ? d : e)
When in doubt or when the expression is complex, use parentheses to ensure you get the result you expect and to make your intent clear to others.
Audulus also offers a number of functions which can be used in expressions. Because functions have a built in set of parentheses, they follow the same rules as other parentheses. The arguments to a function are evaluated first, then the function is called. You can find additional information including a list of functions in the online documentation
