Here’s brief introduction to PM synthesis building on @RobertSyrett’s excellent “Know Your Nodes” series
uPop DX Tutorial Pt 1.audulus (20.2 KB)
uPop DX Tutorial Pt 2.audulus (377.7 KB)
![]()
Here’s brief introduction to PM synthesis building on @RobertSyrett’s excellent “Know Your Nodes” series
uPop DX Tutorial Pt 1.audulus (20.2 KB)
uPop DX Tutorial Pt 2.audulus (377.7 KB)
![]()
Nice! A good old-fashioned interactive tutorial. 
Ha! So right away, in the very first text box I got puzzled. This seemed to help a little:

It always seems like there is something missing in Math though, like I was late for a meeting or something. So you can see in the .gif you get three rads. Fine. Then you have a difference or remainder area which is somehow π ?
We are trying to define the area of a circle?
I suppose there is a periodic object, so there will be cycles. Whether measuring or generating those cycles, there will be a constant – even in variation it would have to be a deviation which would still imply a constant. So is 2*pi the periodic function of an oscillation at a steady rate?
It’s weird, it’s like I want to think that there is a rate of tracing the edge of a circle which is somehow related to its size or area.
That’s how mathematicians have defined π. When we think about phase, we are talking about a repeating periodic function. Since all periodic functions can be described as a cycle, the math of circles is used as part of the vocabulary. Think of the waveform as being a locked groove on a record sitting on a turn table. Where you start can be marked on the edge of the record so the whole waveform is 2π long. So there isn’t area involved, it’s just the circumference we need to think about.
The 2π correlates to length not rate. Suppose a wavetable is 512 samples long. The 512 samples maps to the 2π in the last paragraph.
I don’t think I can properly conceive of the relation between a periodic function and its representation as the circumference of a circle without some sort of fixed time.
I suppose you could say let time=1 day divided into seconds and then treat the size of the circle as being how far you would have to draw a line** from the center to the edge so that if you rotated from the edge point you would return to this start point in terms of the relation between the radius and time as the defined constant?
** this is wrong. It wouldn’t matter how long the line is, the rate of rotation in a period would be the same from anything above zero out to infinity…
I suppose “fixed” should be thought of as ‘relative’ like a ratio, so there is a tension value between members.
The phrase in part one of the tutorial “…pi is the number of radians in a complete circle” throws me off a bit. From the .gif, it looks like pi is a remainder when half of a circle if divided into three equal parts.
All that aside… I moved on through the tutorial and really enjoyed part 2. I definitely learned a lot more about PM synthesis by being able to deal with a modular gui. So appreciated @stschoen!
That’s two times Pi. Pi radians is halfway around the outside of the circle. (circumference, not area). The little section you see at the end of the .gif is the .14159… part of the number Pi (3.14159…)  I guess you could say it’s just a piece of Pi.
I guess you could say it’s just a piece of Pi.
Pi is a ratio. It’s the ratio between the diameter and circumference of a circle. It doesn’t matter what size the circle is, the circumference is Pi times the diameter. Since the radius is half the diameter, the circumference is 2*Pi radians. In this case the time is fixed. The time is the period of the wave. So if it takes 0.5 seconds for the circle to rotate one complete revolution, that would be our period. The frequency is 1 divided by the period, or in this case 2 cycles per second, or Hertz. If you change the time it takes to make one revolution, you change the period and frequency or the wave.
There’s a rundown of the Phasor and the math involved in the Audulus documentation here:
Do you have a copy of the manual in an offline pdf or something somewhere? I don’t see a link on your website for that.
If you print it out, you can either print it to a PDF or to paper directly. Either way, it gets formatted really nicely. If I were to make a PDF version of it right now, that would be all I would do.
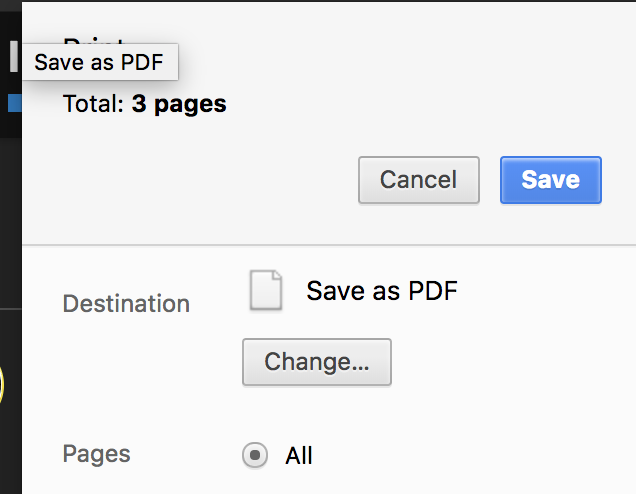
It’s got a lot of animations in it though, so it would be less useful printed out. Soon it will have videos and sounds with it too, so it’s definitely more of a multimedia manual.
It would be cool in this day and age if there was something like an offline multimedia manual. I might be somewhere for the summer where I, quite happily, won’t have internet. I also make a lot of music out in nature, so being able to look through the manual for information, inspiration, etc. while using my iPad as an off grid production studio is my ideal setting.
I will do the pdf save for sure. Maybe file this with the “in a perfect world” list of ideas, as I see one cannot embed a .gif in a .pdf. It would have to be a .mov or something.
You can also save the docs on the Safari reading list. This will capture the html directly and save it locally so you can view it offline.
Forgot to mention that this worked really well and now I have an offline manual with animations.
Starting to dig a little deeper here into the uPop. Why are there 3 phase inputs?
@futureaztec Some of the DX7 algorithms have more than one modulator. The most the DX7 uses on one carrier is 3. The 3 Phase inputs are just added internally so you don’t have to mess with the add node if you want to use multiple modulators. The feedback input has a unit delay and goes through a level control and then it is added as well. The unit delay prevents Audulus from automatically inserting a I frame delay in the feedback loop.
Looking at the traditional algorithms I now see three modulators feeding a single carrier and I understand the 3 phase inputs. I guess I don’t quite understand how the modulators are mixed inside or how the waves interact.
I got a little tripped up earlier in this thread about phasing and time, about pi and radius. One thing that stuck in my mind was that if you draw a straight line from the centre of a circle to the circumference, anywhere on that line with reach the same start point after a full rotation except that the further you travel from the centre, the faster you must travel around the circle. When you look at phase modulation on a oscilloscope there is folding. Is this related to this distance-from-center / speed property?
The unit circle, as used for the purposes of illustrating phase, is fixed. You don’t change the radius in phase modulation - what you change is where on the circumference circle the radius is referencing or pointing to. Make sense?
The modulators are simply added together. This is also the case with the DX7. Because the modulators are added, the relative phase between them is important. With Audulus, phasors of the same frequency that are started together, stay in phase, but you may find it necessary to use the sync input to resync them if you adjust one to a non-integer multiplier then back. Worst case is 180 out of phase which would give 100% cancellation if the waveforms are of equal amplitude. I often use the keyboard gate as a sync signal. The phase issue is why the earlier uPop models used a common phasor as an input rather than each module having its own oscillator. Its also why phase modulation wasn’t really practical with analog equipment. Because the oscillators drifted out of phase, the same patch could sound very different each time you played it. The length of the radius corresponds to the amplitude of the wave. Think of a circle rolling along the ground with a point on its rim and one halfway along the radius. As the circle rolls along, each point will trace out a sine wave. The waves will be the same frequency and in phase with each other, but the wave traced by the point halfway along the radius will be half as large. The “folding” you see on an o’scope is the result of mixing the various harmonics created by modulating the carrier. Depending on the ratio and amplitude of the modulator as well as it’s waveform, the output of the carrier can resemble anything from a pure sine wave to “noise”