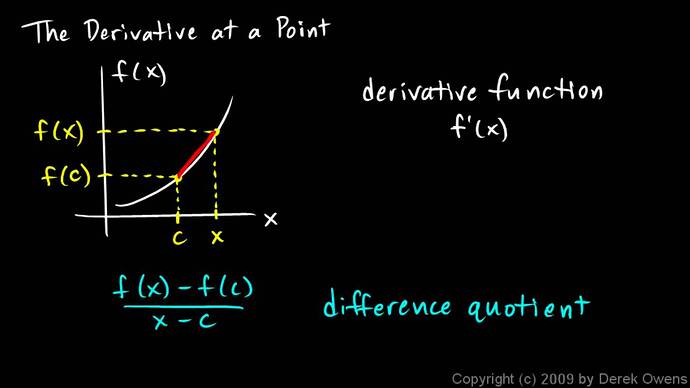After learning about the use of ‘live integration’ for digital filters (brilliantly explained by Stephen here) I spontaneously wanted to create a live “derivator” - meaning a tool that repeatedly outputs the result of [ f( x ) -f( c ) ] / [c - x]
I have access to the value of f(a) since it’s my input. I also have the value of f(b) as this is simply the value of the input delayed by one sample. So far so good.
What I don’t understand is what the values of c and x should be. Since I’m doing this live, x is “now” and c is “1 sample ago”. I tried using x=0 and c=-1 but that seems foolish and it doesn’t work.
Maybe this stems from a poor understanding of the integrators in the first place. I don’t know. I think it can be musically useful to have access to the derivative of an LFO and I haven’t found this anywhere on the forum or Audulus resources.
Any pointers? 
edited with image.
1 Like
@stschoen Thoughts? I’m not sure myself on this one (the math of digital filters still eludes me a bit)
1 Like
As your image indicates, the first order derivative of a function is the instantaneous slope of the graph at a given point. In outr case the the y axis of the graph represents the input to the “deriviator” and the x axis represents time. Since the difference in time between the last sample and current sample is given by 1/sample rate (or 1/41000), the slope from the last sample to the current sample is given by current (sample - previous sample)/(1/41000) or (sample-previous sample)*41000.
Note that since the output is the rate of change between samples expressed in units per second, the value of the derivative will grow very large as the frequency of the signal increases. If we have a 0-1 ramp at 100 Hz, during the rising portion of the ramp the value of the derivative will be 1/0.01 or 100
Alternatively you could calculate the derivative of the change over samples rather than time as is more customary. In this case rather than 1/41000 as the interval you would use 1 since there is 1 sample between f(a) and f(b). This would be (current sample-previous sample). The same curve as the earlier example, just divided by 41000.
derivator.audulus (2.8 KB)
3 Likes
woah, I’m blown away by how quickly you resolved that. THANK YOU!
I see how the frequency affects the value of the derivative. It should be fairly easy to implement a downscaling element that ensures the value stays between -1 and 1 - I’ll try that tomorrow.
Then I need to try this with a bunch of different waveforms and see if it’s useful at all, at audio rate or for modulation…
2 Likes
Actually, since the maximum change between 2 adjacent samples is +/-2 (-1 to 1 or 1 to -1) then if you use (current sample - previous sample)/2 you will never exceed -1 to 1. However using this expression the derivator will output very small values for smoother waveforms. In my previous example I noted that a 0-1 ramp at 100 Hz would output 100 during the rising portion of the waveform, but failed to mention that it would produce a -41000 spike at the end of the ramp (assuming a single sample drop from 1 to 0). If you scaled it using this formula, the spike would be -0.5 but during the rest of the ramp it would be 0.0012. Since the value of the derivative is based on the shape of the waveform as well as its frequency, scaling it might be difficult. You could try using a low-pass filter to do some slew limiting since large outputs will be in the form of spikes rather than sustained values. You might get a more useful output, although integrating the derivative could end up being an exercise in futility (lol) 
3 Likes
Can you use this black magic to make a better version of a rising signal indicator?
1 Like
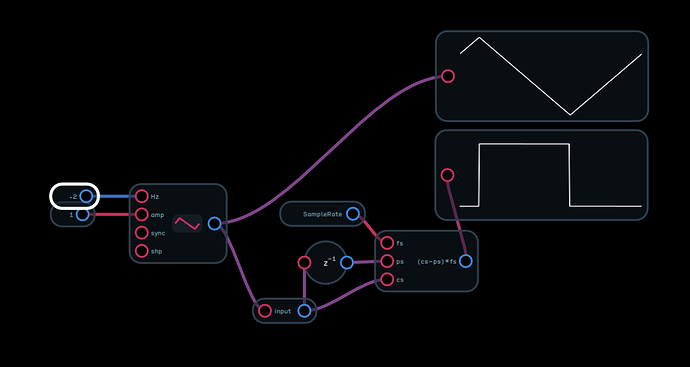
Actually any time the derivative is positive the signal is rising so it would certainly serve. The patch I posted uses the z-1 node in a feed forward configuration so it wouldn’t have worked before the last update where @taylor added that functionality. Really all you need now that the z-1 works feeding forward is to compare the z-1 output and the the current sample. If the current sample is larger, the signal is rising.
3 Likes
Oh! It was just a comparator away! Interesting, this is definitely something to experiment with.
2 Likes
I quickly threw together a version of your derivator with variable “scaling”. It’s just a knob that divides the derivative by some number, up to 1000. This seems much more usable and as you can see in this patch, you can derive some seriously pretty waveforms from a complex LFO!! I’m stoked, this was pretty much exactly the type of stuff I wanted to end up with. Just look at 'em wavey waves 
derivator-with-scaling.audulus (13.0 KB)
edit: well, the thing about derivation is that it’s only fun with polynomial or sinusoidal functions. obviously, sawtooth, triangle and square waves derive into uninteresting shapes, since their rise/fall is constant. I tried this with a random LFO (noise->s&h->slew limiter) but it wasn’t nice either (maybe a smoother slew limiter is required). I’m still going to try and make this into a proper module, some kind of LFO or something.
2 Likes
Pretty neat output waveforms. 
![]()