Does anyone have an allpass filter that can shift all partials 90 degrees?
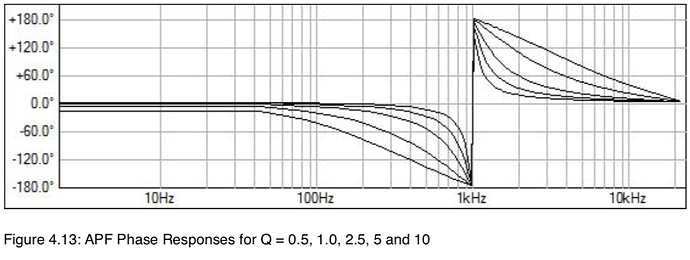
If I understand you I’m not sure if that’s possible. Usually an all-pass has some kind of a curve to the phase response. This is the phase response for the SVF based APF I built from Pirkle’s paper.
uAPF V1.2.audulus (34.4 KB)
Thanks, I think that makes a fair amount of sense. If I wanted to split a signal into multiple bands and process each separately to 90 degrees, how many bands do you think would be optimal?
I guess it depends on what you’re trying to achieve. You could certainly use a set of bandpass filters with appropriate center frequencies followed by a set of APF, although the bandpass filters will also introduce some phase shift. Sounds like it might be fairly CPU hungry.
This is for my iPad Pro, and it’s a dedicated patch to go with the modular. I’m looking to make a frequency shifter not based on the Hordijk one.
OK, now you have me intrigued. How would it work?
It’s more or less the same principle based on trigonometric identities regarding the summing of frequencies. I will elaborate more when I am not on my phone.
This is all in relation to a conversation I had with a redditor by the name of x2mirko. He is excited about the possibility of a Serge frequency shifter. Which is the same in principle to the Horidijk frequency shifter but with a different filter structure. The basis for frequency shifting starts a sinusoid.
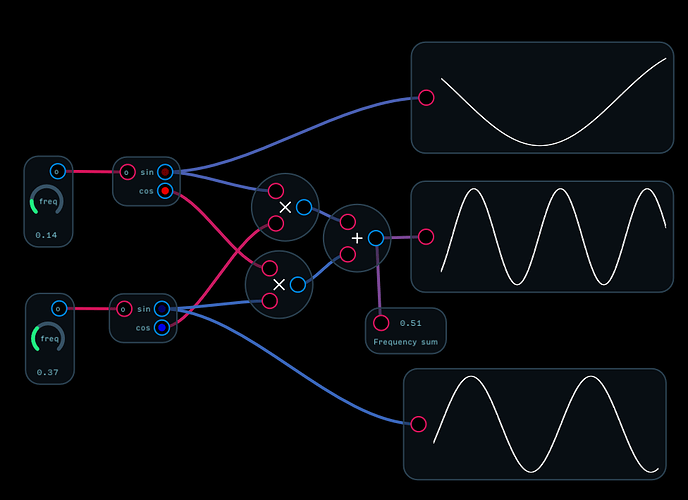
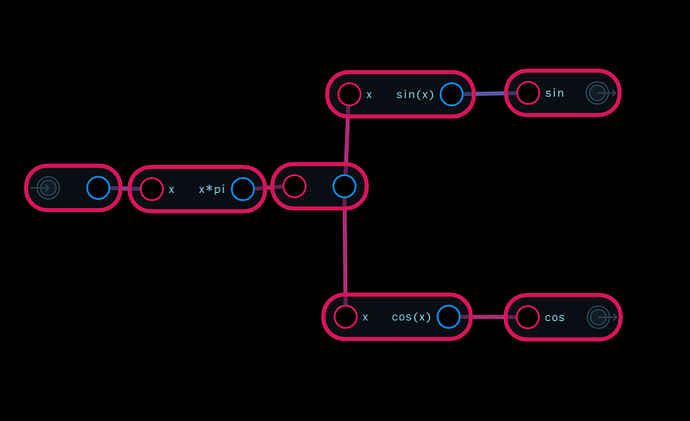
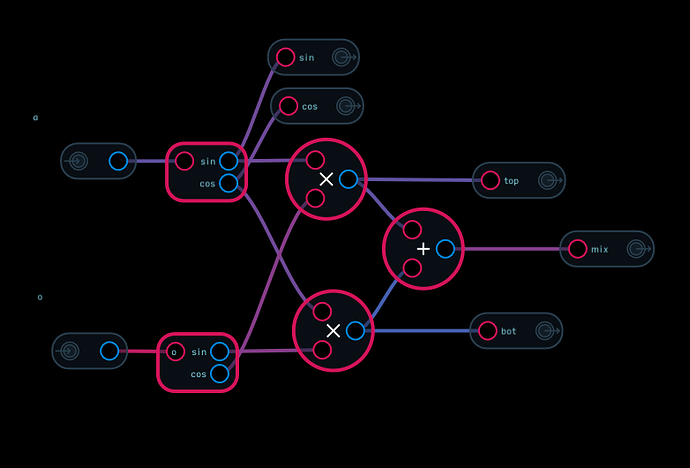
sin(f1 + f2) = sin(f1) * cos(f2) + sin(f1) * cos(f2)
frequency shifting with sinusoids.audulus (29.2 KB)
In the analog realm, for radio tech, there was a device that had a modulating oscillator that shifted the frequency of an incoming signal. Of course it is simple to get sin and cos of the internal oscillator, but how do you obtain the cosine of an arbitrary signal?
x2mirko explains:
"Phase shifting can of course be done with an allpass filter, but it’ll only give you an exact 90 degree shift over a certain frequency range, so the signal needs to be bandlimited (or you need to split it into multiple bands and process each separately).
Once you have the phase shifted signal, you can calculate the two products using ring modulation and just sum them together - The ring modulators will generate sidebands at the sum and difference of the frequencies, but since you have used phase shifted copies to feed them, the upper (and lower respectively) sideband will cancel out when you sum them up (which just shows how exact the phase shift has to be)."
“There’s also other implementations that are more common in radio tech, where you just multiply your signal way far up (out of audio range), then filter out one of the sidebands (which is easier because due to the huge second frequency the sidebands don’t overlap so much) and then multiply the sideband that survived with another high (but slightly lower) frequency such that the lower sideband is back in the audio range (and a shifted version depending on how you chose your two modulator signals). But from what I understand, it doesn’t work so well for tiny frequency shifts (which are most interesting for synthesizers) because you need two very exact oscillators running at very high frequencies.”
The second approach seems like it might be interesting to try once oversampling is a thing, but phase shifting a signal with band-limited segments in parallel seems possible.
Except that I’m still not up to speed with filter math ![]()
I wonder how the built in pitch shifter works. In the digital realm I would think it would be easier to simply remove some percentage of the samples. Of course doing this in real time isn’t trivial either. From looking at the phase response plot, it would look like a low Q would give you the widest range of frequencies close to 90 degrees. If I recall correctly the graphic EQ I built a while back had 1/2 octave bands. I would run a sine at the center frequency through each band and adjust the APF center frequency for a 90 degree shift. That should allow you to compensate somewhat for any shift introduced by the biquad bandpass. Actually the filters are peaking filters but they should be easy to replace with bandpass if necessary. Here’s the EQ ands a convenient collection of biquad based filters by Robert Bristow-Johnson.
Biquad filters.audulus (102.9 KB)
equalizer V1.2.audulus (181.1 KB)
Amazing! This should keep me busy for a while, many thanks!
The DSP is for digital pitch-shifting is mostly granular. Ableton Live has a couple different modes, one where it detect transients (or if it’s recorded on the grid you can set it to regular intervals like 16th notes) and it truncates each grain or plays a backwards loop. The other mode is more like it rapidly crossfades between grains and is like a sonic equivalent of the stamp tool in photoshop.
I would be curious as well to know what mojo the Audulus pitch shifter has going on.
Sadly it sounds almost identical to ring modulation 
I think over all @RudigerMeyer’s Frequency shifter sounds more interesting and doesn’t use 55% CPU.
What ended up being more interestingsonically was scaling the audio input to +/- π and running it through sin and cos expressions before doing the dual ring mod and sum trick. This way if you feed it a sawtooth it will be classic radio frequency shifting and other sounds will be interestingly mutated.
It sounds convincingly FM like and weird.
Interlude on Moonbase Alpha.audulus (817.2 KB)
I’m not surprised that it sounded a bit ring modulated. Getting narrow enough bands and 90 degree phase shifts sounded like it might be tough. I guess you were still getting a lot of uncanceled side bands.