Hi All,
First post on the new forums! Love the Audulus community. You guys are great. Was wondering a few things:
a) What’s the difference between wavefolding and waveshaping? Is it just a semantic difference, or a practical one?
b) I’m curious about the math behind tube, FET, Serge, and other “analog” type distortions and shapers. Where do I start?
c) On the old forum, a user had like a whole huge patch with hundreds of waveshaping expression nodes (I think it was Syrett). Any chance that user could re-upload that patch or offer some directions to start off in?
d) A user uploaded in a very brief response to a thread the Serge style wavefolding algorithm and I can’t find it anywhere. I would love to track down this little tidbit. (On a slightly related note, I can’t get the old forum to render, it could be a mobile issue. It’s not dead, is it?)
If you would like a more practical use case for background, I’m building a single voice and want some nice harmonic manipulations of basic waveforms to test out. No example patches yet as I sort of split my time between Audulus, Pure, and Max. Thanks in advance.
p.s. Not totally familiar with the categories so if this is in the wrong spot, feel free to move it.
1 Like
Hello @inscript, and welcome to the forum. I love messing about with waveforms also! Let me see if I can answer some questions.
a) All waveforlders are waveshapers but not the reverse. Waveshaping is simply the process of changing the periodic waveform of an incoming signal. Other examples of waveshapers could be full wave rectifiers (turning a sawtooth into a triangle) or a comparator (turning a sawtooth into a pulse wave). Wavefolders come in many designs but they usually describe a wave the reflects back towards the center rather than clip.
b) I think start with trigonometric functions. tanh(x) is a very useful expression for creating saturated distortion because no matter how much you scale x (you could amplify it 10 times even) it will never clip, since the tanh(x) never reaches one. sin(x) is also a pretty useful function since it naturally acts as a wave folder in the same way that tanh(x) will act like soft clipping amp. Hard clipping can be done by simply clamping your signal with an expression like clamp(x,-1,1).
c) Sounds like something I would do, I would be happy to post some example patches, although I 'm not sure which ones you are referring to.
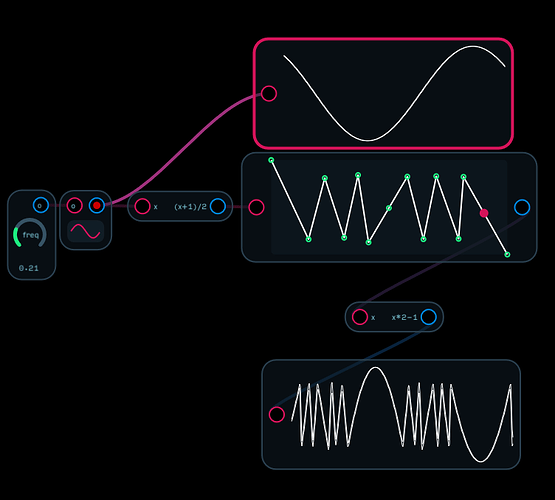
d) I think the best way to emulate the serge wave folder is with the spline node and a little low pass filtering above 2kHz. There were some academic papers related to serge wavefolders that show what you want your spline to look like:
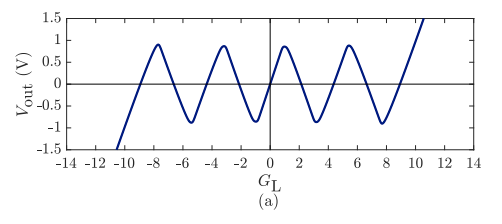
In practice, a sin(x) expression sounds very similar and is much easier to work with.
Yeah, that’s loads of fun. I like to make cascaded crossfades of waveforms using switches. You might enjoy my “Know Your Nodes” videos on youtube where I go over some of these topics.
I will upload some examples shortly.
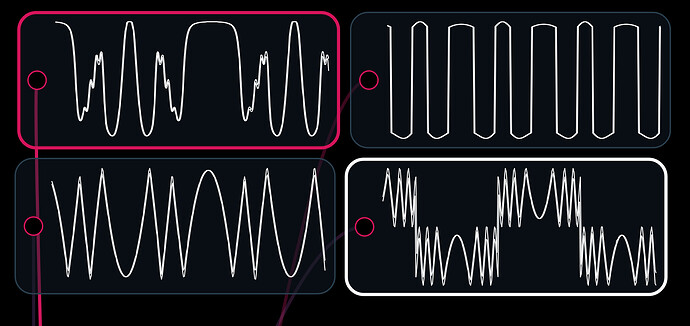
Ok, so here are the tasters choice of wave folders I have in my collection:
All of those signals went in as sine waves.
4 Wavefolders.audulus (129.9 KB)
Definitely feel free to open them up see how they work, and incorporate anything you find useful 
PS if you have trouble with the forum downloading patches on iOS check out the workflow app. @Paulenko made helpful video guide.
2 Likes
And if you’ve updated to iOS 12, Workflow is now the Shortcuts app.
1 Like
For what it’s worth here’s the Hordijk waveshaper that I put together using one of @robertsyrett’s waveshapers (using the sin(x) function) as a starting point.
If you’re having problems with the old forum not rendering a possible cause could be that you’re using an (ad)blocker of some kind. At least that’s what happened to me when the forum shifted to the new discourse version. Whitelisting it should bring it all back.
1 Like
Yeah, that’s a well-written post for sure!
Awesome. Thank you for the responses. This provides some great starting points. @robertsyrett I actually just watched all of your video series. Those are super useful, and exactly the kind of thing I’m looking for. I’m working my way through the Serge white paper. Does anyone have any resources on how to begin converting analog schematics into digital block diagram models? Seems like a bit of a daunting process, and I have very little familiarity with the analog EE side of things. @RudigerMeyer I’ve browsed all of your Hordijk clone threads, super high quality work, and the explanations are great. Look forward to getting through all of that seminar video series.
3 Likes
The easiest thing is to find the block diagram of the model rather than try to create one from the schematic. They aren’t available for all synth modules, but for lots of them.
We’re not doing component-level modelling in Audulus, which would get you the most accurate representation (and consume a lot of CPU), but what you can aim for is to make it close enough. The best thing you can do to really nail something in Audulus is to tune the way the filters and distortions work within a circuit by comparing them to one another in an A/B listening test.
This is above my pay grade, but I’ve become really interested (thanks to 0-Toast which led me to some 0-Coast demos) in the wavefolding used in Buchlas – it is both powerful and musical. It has a character that is great. Anyway, while poking around to see if I could learn something that I could use to implement a similar wavefolder in audulus, I found this paper (co-authored by a guy from Native Instruments). I don’t understand the engineering well-enough to be able to do anything with the information. But maybe someone here could? (The topic is digital modeling of the algorithm).
http://www.dafx17.eca.ed.ac.uk/papers/DAFx17_paper_82.pdf
I mention it in case someone with skills could make use of it.
Thanks. I’ll check it out. I have been enjoying exploring the West Coast example here (in fact, that is what has sent me down the rabbit hole), but there is a certain family of timbres that I haven’t succeeded at reproducing. I am hoping to figure out how to do re-purpose parts of the various projects to see if I can get closer.
The family of sounds in the neighborhood of what Todd Barton demonstrates here: (at about 5:50)
1 Like
I am slowly making my way through more systematically comparing various wavefolders (and examples of wavefolders in action – via recordings I am finding) in Audulus and various soft synths.
With this spline-based wavefoldng, what would the correct way of turning up the wavefolding amount (i.e. simulating raising the Timbre slider on a Music Easel or turning up Multiply on an 0-Coast)? I assume that simply crossfading from the the uneffected waveform to the fully-effected waveform is too simplistic – or am I mistaken?
1 Like
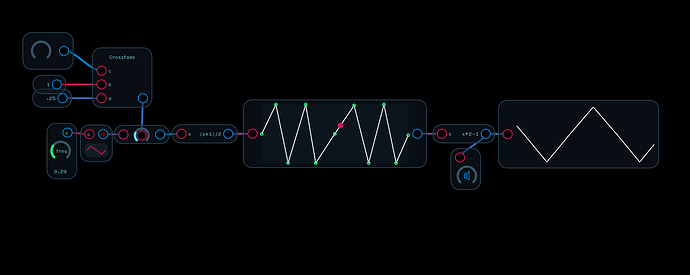
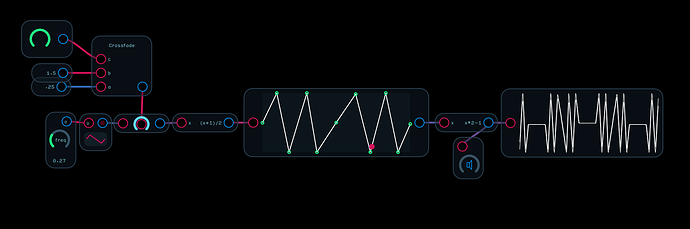
That would be just a mix knob.
You just control the amplitude. Because the spline recreates the original waveform in the center, a low amplitude signal should emerge as more or less an unaffected signal. Then you increase the signal to hear the wave fold. You can even go past 1 and the spline will model the distortion of the analog wavefolder more closely than the sin(x) version.
spline wavefolder explaination.audulus (17.1 KB)
1 Like
Thank you. I was just doing at a spectrographic comparison of a the Buchla 261e folding so that I can compare it to the other examples that I am collecting. Something interesting about it is that as you turn the folding up there are two particular harmonics that get emphasized and even dominate. First comes the harmonic (in my case F#1) that is an octave and a fifth (C#3) higher followed by a harmonic two octaves plus a third (A#3) then D#4! What is interesting to me is the they that the harmonic “density” does not become overwhelming.
Here is a picture.
The Aalto wavefolder (which is also nice and rich) has a much denser profile. You don’t have the same sort of de-emphasis of the lower harmonics as the folding is cranked up:
The wavefold in the Arturia Music Easel:
I need to track down a good sample of an actual Buchla Easel
2 Likes
Interesting! I should point out the spline in example I posted is something I drew just now. If you take greater care to accurately recreate the curve in my previous post, results should be more similar.
https://discourse.audulus.com/t/wavefolders-shapers-and-clippers/1008/10?u=robertsyrett
1 Like
Thanks for pointing that out. I will spend some time trying out different variations of the splines splines. I have a few more wavefolding examples that I want to track down and analyze (in particular the 0-Coast) to get a sense of their profiles and what makes them tick. The sixth that shows up in the Buchla is so cool – and the way the density stays similar is cool.
2 Likes
oh great, I needed this thread! I’ve been making a clone of the Instruo Cs-L eurorack module and got stuck for a while at the wavefolder. I’m still stuck but at least I got something that sounds harsh enough. The Buchla 259 emulation doesn’t sound right to me, so I added some stuff to make the folding sound harsher. Here’s the result.
my-weird-wavefolder.audulus (9.7 KB)
2 Likes
Looks good! Using the absolute value expression as a full wave rectifier will definitely get you some additional harmonics.
2 Likes
Have you figured out ways to implement a “symmetry” control? I don’t know how common it is for wavefolders to have that. On the Instruo Cs-L, there’s this knob that seems to control “where” the wavefolding happens - at 50% both the top and bottom of the wave are folded equally, at 100% only the bottom and 0% only the top. At least that’s what it sounds like to me…