Noise Osc: Noise and Stepped Randoms
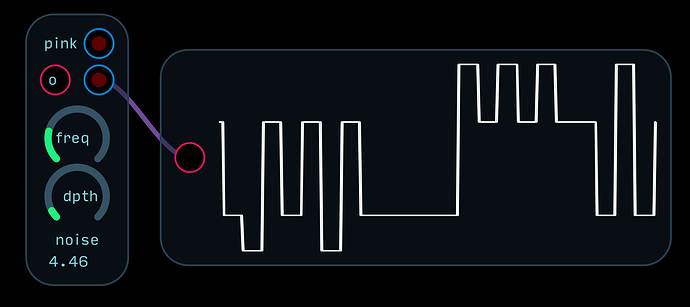
At it’s heart, Noise Osc is a square wave oscillator driving a sample and hold connected to a bipolar noise source. This signal is then fed through a bit crusher. There is also a separate output that is also sent through a pinking filter to tone down the high end of the frequencies.
The technique of changing the sample rate and the bit depth is big part of early video game sound effects, so Noise Osc is the perfect tool for creating percussions for your chip tune compositions.
This is a complete rebuild of the uNoise module I made last year and has improved balancing of the frequency and depth controls for more intuitive sound exploration. Noise has never sounded crunchier!
I/O
| Input |
Signal Range |
Notes |
 |
-5 to + 2 |
Tracks 1/octave to the frequency knob value. Sending modulation to this input will also yield exponential noise sweeps. |
|
|
|
| Output |
Signal Range |
Notes |
 |
-1 to 1 |
The main out is a harmonically rich noise source as there is a periodic component that a stepped signal has that is absent in true white noise. |
 |
-1 to 1 |
The pinking filter will considerably mellow the sound of the Noise osc output at higher frequencies and will lightly slew the output at modulation frequencies. |
Controls
| Knob |
Function |
Notes |
 |
Reference Frequency |
Set the knob to .5 to set the reference frequency to 440 Hz, which is the standard for 1/oct signals. Sweeping to the left will quickly bring you to modulation rate signals while a turn to the right will sweep up to 20 KHz. |
 |
Bit Depth |
The bit depth parameter continuously sweeps from 2 to 256 discrete signal depths and then crossfades to an un-bit crushed signal. |
Displays
| Meter |
Displays |
Notes |
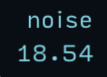 |
Noise Frequency |
Displays a Hz Value |
Version History
| Revision |
File |
Date |
Notes |
| 2.0 |
Noise Osc.audulus (17.9 KB) |
2018/07/14 |
update of uNoise module. |
5 Likes
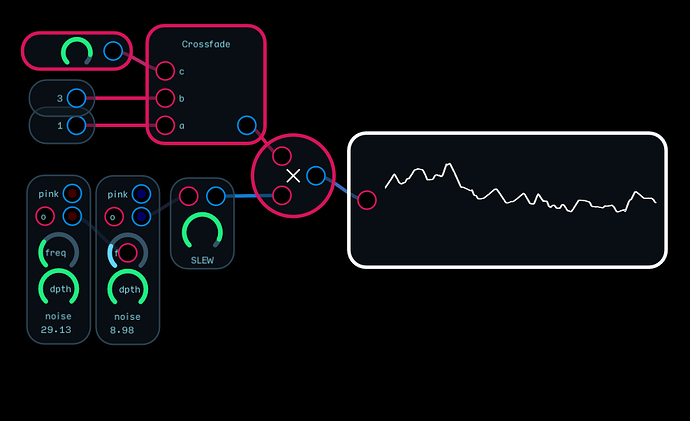
smooth random.audulus (48.4 KB)
Here is a configuration of the Noise Osc to produce smooth randoms akin to those you would find on a Buchla Source of Uncertainty.
3 Likes