I thought I’d gotten through all the Hordijk Modules, but of course there’s always one more thing…
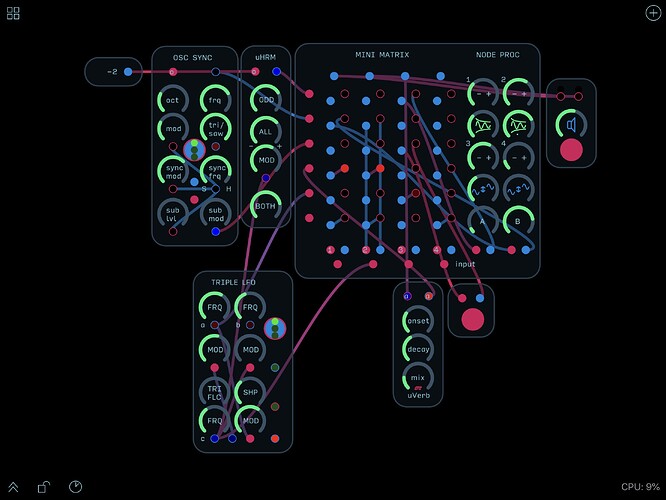
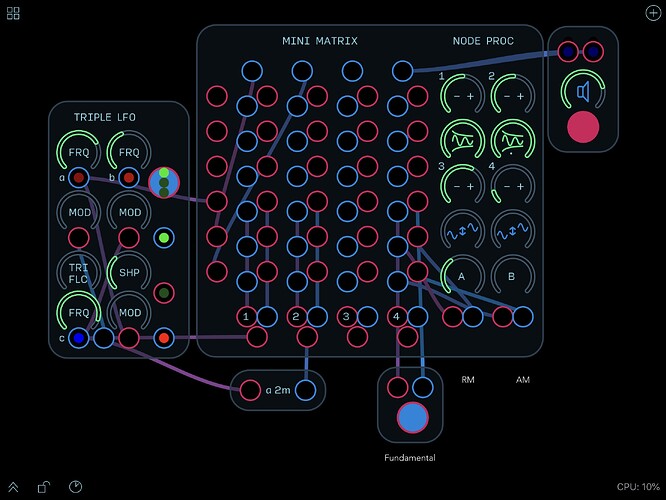
Inspired (like much else with Hordijk) by the EMS Synthi/Putney he gives his own take on the use of a matrix within a modern context.
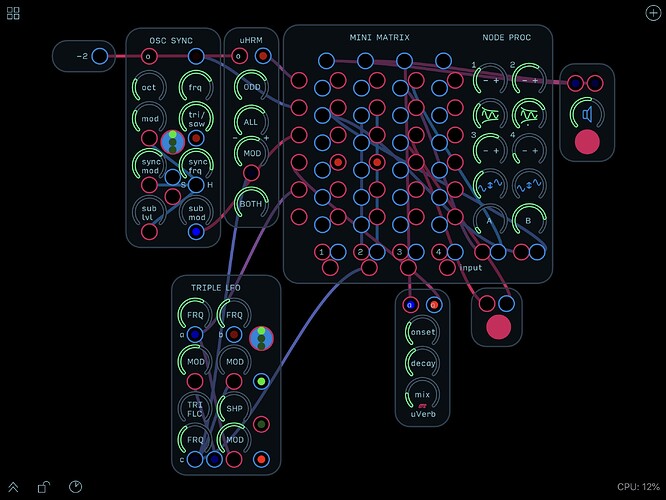
Hordijk’s innovation is to use the well established technique of using a stereo cable to provide an insert point, here applied to each node in the matrix. This means that instead of a simple on/off connection, a level control or other kind of (more complicated) effect/processing can be applied to each node. Hordijk includes two level knobs as well as some ‘node processors’ alongside the matrix ready to be patched in for this purpose, but external sources can but used just as well. Concerning the size of the matrix itself (and the balance between flexibility and usability) he finds that a 6 x 4 grid is well suited to a typical 12 module (4 panel) Hordijk system since connections can also be made directly without necessarily having to go through the matrix.
I’ve been experimenting with how to set up something similar in Audulus: Stereo cables, the key element, are possible in Audulus, but unfortunately only in a single direction, i.e. it isn’t possible to use a single cable for both a send and a return. This means that one has to resort to manually making both parts of the connection, which is not quite as elegant as a single stereo cable and can easily get visually messy and confusing, even though it does open up even more possibilities for routings. (One trick that I’ve found useful to check on which connections have been made, is to zoom out slightly so that one shifts out of connection mode on iOS.)
Following Hordijk’s example, I’ve included 4 bipolar VCAs (using @RobertSyrett’s Audio Attenuator) for the ‘node processing’ – bipolar for the ring modulation and echo-like effects that they make possible, as with the Dual Fader. In my version VCAs 1 & 2 have controls to adjust the amount of modulation applied via the modulation input, and 3 & 4 have controls to adjust the offset, which also makes them useful for scaling unipolar modulation signals.
As Hordijk points out a matrix can be useful not only for mixing signals, but also distributing them (multiples), as well as creating complex (multiple) feedback loops.
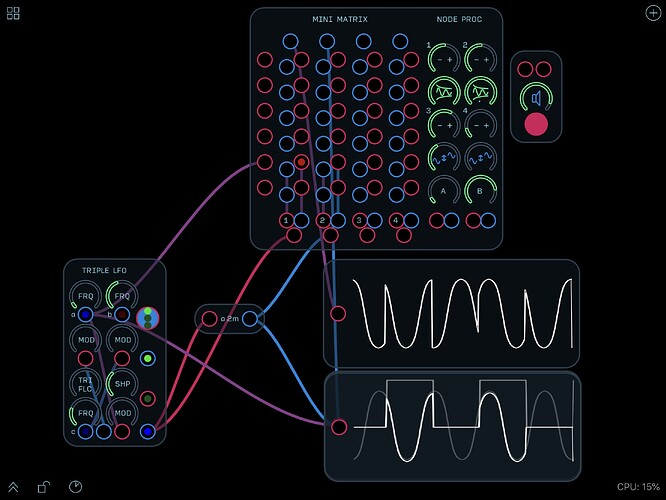
Here’s a simple demo:
RH-RM Mini Matrix - Node Proccessor v.1a Demo.audulus (394.4 KB)
And a basic version without the node processors:
Basic Matrix.audulus (24.9 KB)
4 Likes
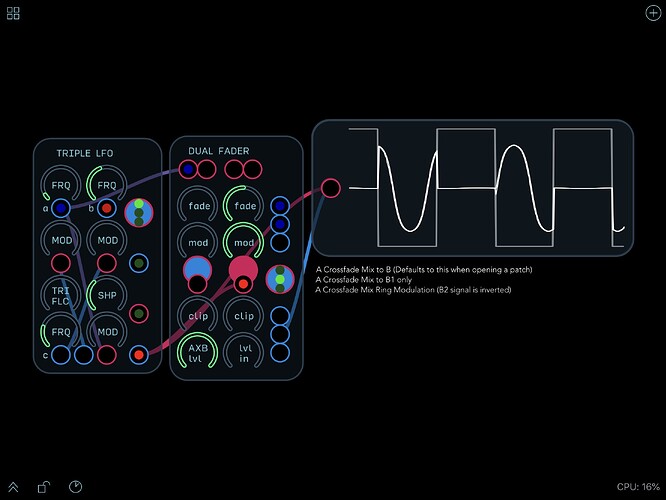
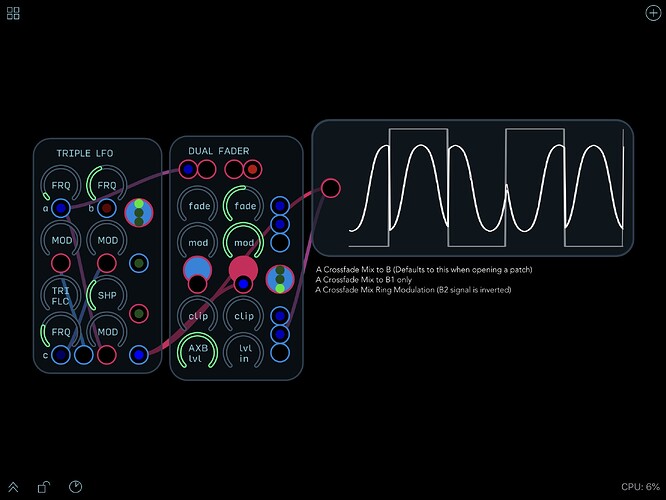
Rob Hordijk includes bipolar VCAs as part of both the Mini Matrix Node Proc and the Dual Fader, and has demonstrated, in the various videos for these modules, the ring modulation effects that this makes possible .
Via a recent Reaktorplayer tweet I came across a nice Learning Modular tutorial demonstrating the difference between amplitude and balanced (ring) modulation.
Towards the end of the tutorial there’s also a nice demonstration of the way in which the fundamental of the carrier falls away with ring modulation but remains present with amplitude modulation.
Following the Learning Modular video, I put together some simple demonstrations using both the Mini Matrix Node Proc and the Dual Fader.
RH-RM Mini Matrix - Node Proc AMBM Demo.audulus (221.9 KB)
RH-RM Dual Fader AMBM Demo.audulus (160.2 KB)
(Use the Dual Fader selection switch to shift between amplitude and ring modulation)
And a version at audio rates: (Knob A to set the level for ring modulation and knob B for amplitude modulation) RH-RM Mini Matrix - Node Proc AMBM (Audio) Demo.audulus (223.6 KB)
4 Likes
Following on the post above on bipolar VCAs: Since there are some similarities between what’s going on with bipolar amplitude modulation and through-zero frequency modulation I thought I’d take a another look at these topics in a little more detail.
Learning Modular has a nice post on Understanding the Differences Between Exponential, Linear, and Through-Zero FM, and from there I revisited @RobertSyrett’s Know your Nodes video on Comparing different types of FM.
One aspect that through-zero FM and bipolar AM modulations have in common is that they don’t freeze (or shut-off) output when the modulation signal falls below zero. Both do this by inverting the waveform in question. In the case of TZFM it is not the amplitude that is inverted but the phase of the waveform: In the Learning Modular video Chris Meyer describes this inversion as the oscillator ‘running backwards’ while @RobertSyrett in his Audulus demonstration talks of a reversal of the direction in which the waveform is being read. This means that there can be sudden changes in the direction of the waveform (in addition to it being sped-up/slowed-down) but without the potential jumps at the point of inversion that can occur with bipolar AM.
With both types of modulation sidebands are generated and this results in a change in the harmonic content of the waveform. In my previous post I noted Chris Meyer’s demonstration of the way in which the fundamental of the carrier falls away as bipolar AM (ring) modulation is increased, but remains present with amplitude modulation. Similar processes are at play in FM (of all kinds) and I came across a series of old Sound on Sound articles, one of which includes an good explanation of how the Bessel function can be used to describe the amplitude of each pair of side bands, and how they relate to the strength of the other partials and affect the relative strength of the fundamental.
@RobertSyrett demonstrates in his video how with TZFM sweeping the frequency also changes the character of the Bessel function (i.e. the timbre of the sound), while with PM the character of the Bessel function is uniform across the frequency range since the phase is not calculated in relation to the hertz value of the modulator – i.e. the timbre/harmonic structure of the waveform stays the same across the frequency range.
Phase modulation differs from TZFM in that the modulating waveform also changes the starting point of the carrier waveform. With TZFM the carrier remains in phase with modulating signal (through a continuously morphing Bessel function).
4 Likes
Love the links. There is nothing like digging into the archives of SOS and finding some old school diagrams. The Bessel function gif in the Wikipedia article was also pretty striking with it’s drum head analogy.
I should clarify that everything above is most evident in the case of a 1:1 carrier to modulator ratio. While the flavor of difference is still audible with other ratios, it will not look as clean on an oscilloscope. I just chose 1:1 for the example because it is a special case that clearly shows the difference in general.
3 Likes
Thanks for putting this all together. I was really wanting a detailed experimental video with a good scope. The guy is such a great, clear presenter. I must say I did like the “grunge” on the digital TZ oscillator chip!
2 Likes