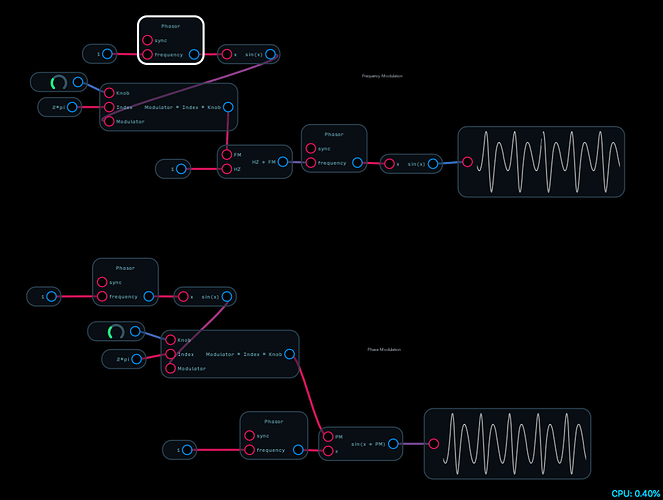
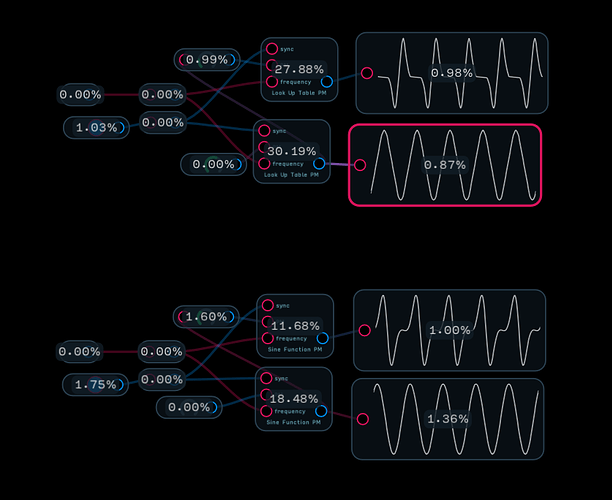
I was just thinking that @robertsyrett demonstrates that while they may be described as being mathematically ‘equivalent’, there is a difference in practice (even if it isn’t a very big one).
Like you (and @robertsyrett in the video) said: linear fm and pm are mostly the same when using sine operators but there are some little differences.
When the frequency of a pm operator is increased it scrolls faster though the phase of the carrier which results in stronger frequency modulation. This doesn‘t apply to frequency modulation.
So the first difference is that the depth of phase modulation increases with the pitch of the operator and that the depth of fm doesn‘t.
A second difference I can think of is that not all oscillators that can do linear fm can also do trough zero fm. The modulation in frequency that‘s caused by phase modulation always is trough zero.
Here a little demo so you can hear the differences:
pm vs. lin fm.audulus (30.8 KB)
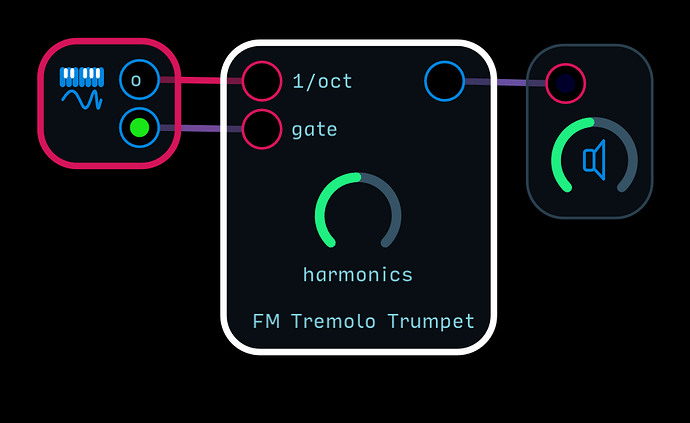
I had a go at recreating the synth brass patch form the video above and ended up making an interesting tremolo trumpet sound.
FM Tremolo Trumpet.audulus (126.7 KB)
That’s a gem
Another nugget. Thanks.
I’m still working on FM patches. I will probably make a collection of preset synth voices that respond to modulation at some point.
I found this series very useful as well:
The classics!
Of course no FM thread would be complete without a scan of a photocopy of the 1986 classic book on FM Synthesis by Chowning and Bristow.
But the fun doesn’t stop there! I found great blog post about shaping your wave frorm with the sine function.
Very interesting. I hadn’t read Chowning’s paper before. One point he makes early on, starting on page 57 is that in order for the index to remain constant the modulator level has to change inversely proportional to the modulator frequency where Index = delta f/modulation frequency. Delta f is the frequency swing caused by the modulator which, for linear FM, is proportional to the modulator level. None of the modules I’ve constructed adjust the modulator level as a function of modulator frequency.
I think that isn’t an issue with phase modulation, but if you want to make frequency modulation behave like phase modulation then you would need to do that.
Chowning”s paper seems to treat the two interchangeably. He specifically references the Yamaha DX7 when discussing the modulator index.
The type of FM that went into the DX series synths is what Chowning had been working on and refining for years. The architecture and algorithms as far as I know were not just inspired by his work but designed by him anc his team at CCRMA. For most musicians at that time, programming FM sounds meant doing it on a DX. It makes sense to that the book is about that.
The Casio “phase distortion” synthesis has a pretty interesting spin on how they allowed their “modules” (their version of operators) to be routed. Definitely worth exploring further.
An interesting overview of the difference between PM and FM:
For a pure sine or cosine modulator the FM and PM are the same, however this does not apply if the modulating wave is something other than a sine or cosine.
I think the number one reason why I prefer the PM implementation of the synthesis method is that I can use it as an LFO waveshaper. When I use FM I get too much of a sweep in frequency rather than a change in the shape unless you very carefully mind the index.
Also, it occurs to me that I haven’t uploaded a basic example of FM vs PM for people to mess around with.
FM vs PM.audulus (4.9 KB)
I enjoy making bold claims and being told I am wrong:
Frequency modulation has to do with multiplication, whereas phase modulation includes factoring. This is because the referent is moving a speed which is variable to the speed of that which refers or has a relationship to it; that is, in terms of modulation, we could say that phase counts as the measure of difference between two periodic subjects. But we know from Einstein that this idea somewhat assumes a God’s eye view of things. In other words, there must be a third frame of reference by which to ground the relationship between any two points in motion in order to discuss their phase.
Am I close?
Ignoring relativistic effects, frequency only requires access to a clock, so one can measure a frequency in an absolute sense. That however doesn’t imply that a frequency is constant with respect to any observer. The Doppler effect is demonstrates that frequency is also relative to the observer’s velocity with respect to the medium in which the wave is propagating. Two observers will only agree on a frequency if they are both stationary with respect to each other. However you are correct regarding phase. In the most common usage, phase is the relative displacement in time between 2 waveforms and therefore is not an absolute quantity. In the case of phase modulation, the referent is the unmodulated waveform so when we speak of modulating the phase, we are implicitly referring to the phase relative to the phase of the unmodulated signal.
Consider an observer measuring a sine wave emitted from a speaker at some distance. If the observer moves toward the speaker he will observe that the frequency of the sine has increased. However is it equally true that he could consider this as a smooth increase in the phase of the wave relative to what he was measuring while stationary. Similarly if he moves away tboth the frequency and phase will decrease.
If the modulating signal is a sine or cosine (or other periodic exponential function), it follows from the math that phase modulation and frequency modulation have the same result. With respect to a DX-7 this would only apply when you have only one modulator modulating a carrier. When you chain modulators so that operator A modulates operator B which modulates operator C as the carrier, this no longer applies to C, since the modulating signal is now no longer a simple sine.
Of course the above analysis only applies to an ideal signal. In the real world, there is no perfect sine, modulations are not truly linear, amplification inevitably results in distortion etc. so in either case the end result is only an approximation to the mathematical ideal. Otherwise two synths based on the same fundamental math would sound the same. No one would argue that all 24 dB filters sound the same, but if they matched the mathematical ideal, they would be indistinguishable. A pure sine is really rather boring. It’s the imperfections that add character to our electronic instruments, so in the end, if it sounds good, it doesn’t really matter too much how it works. ![]()
As I understand it, in mathematical terms frequency is the first-derivative of what we are calling “phase” (I put it in quotes because I have seen some mathematicians say that we aren’t really talking about phase but the angle argument of the sine function). As I understand it, the reason that Chowning and company used “phase modulation” to implement FM was that it was more straightforward to compute using PM (though I am not sure why). Since they were using sine waves, the results were equivalent.
Yeah, I have heard many times that the idea was they only has to store one high resolution look-up table of a quarter of a sinusoid that is mapped 0-1. The operators are triangle waves sweeping that one quarter sine wave back and forth. Calculating phase in a system like this can all be done with simple addition and rounding. That said, when I create this arrangement in Audulus using scaling expressions and a spline to approximate a look up table it is definitely not less CPU intensive than a sine expression.
I think just sticking to sin(x+phase) is the least convoluted way to think about it. The mathematical basis for it is so well understood and the more you traverse the unit circle and the imaginary number plane the easier thinking about this all becomes.
in terms of CPU load, calculating a sin() (or cos(), log(), etc.) are expensive operations. When CPU’s were a lot slower, look-up tables for transcendental functions were very common. Why perform an expensive calculation when you can pre-calculate the result and store it. Even today, the Novation Peak and Summit use look-up tables to generate their basic waveforms. By running the sample rate up to 24 Mhz they eliminate many of the drawbacks of wavetable synthesis. In the case of Audulus, we don’t really have an efficient way to store and access a table of data so this approach isn’t practical for the moment.
Your spline-based approach is a clever implementation, but suffers from the fact that the spline still has to perform linear interpolation between the data points. If there were a way to store a set of samples and access them efficiently, You could probably beat the sin() in CPU load.