Polyrhythmic Tap Sequencer

[dcLargo]

V9/13/18-1

Now that I have a scale-driven mechanism for deriving chord tones, I decided use that feature to simplify the sequencer. The 25-bit quantizer goes away. Tone loop one uses the lookup part of the quantizer, so I made a version with only the queries, “how many tones (degrees) are there in the current scale” and “what is the nth tone on this scale?” Tone loop 2 still uses a quantizer.

Losing several unnecessary quantizers made it possible to use my 16-step progressions machine. There are three ways to run a progression—midi keyboard, seven-button and octave knob widget, and progression machine. With the simpler progression controllers the overall project runs at about 75% of the processor load of my most recent upload. (Remember to hit the “-key” button if you’re using rhe midi input.)

The most obvious change is the method of chord input. I made a big patch board to connect major scale intervals to one or more sequencer steps, up to 16 steps. Instead of some big switch matrix thing, I just made a place to connect a chord tone to one or more sequencer steps. The steps get to the sequencer via a 16x1 mux. The arpeggiator and the random tone generator now just select mux inputs to get a new scale tone.

To derive triads from scales, you look at scale tones, starting at reach tone of the scale (the root tone of the standard 1-3-5 triad) and counting off to get the triad and its extensions. To implement this, I decided to rotate the current scale by however many steps to place the current tone as step one. If I want a third, for example, it’ll be a minor third for some positions on
the scale and a major third on others.

I haven’t done exhaustive testing, but it does appear to be working.
2 2 loop polyrhythm tone seq chord apregg v 9.12.18-1.audulus (2.4 MB)

[dcLargo]

version 9/15/19-1

Nagging errors. To get something I could wrap my head around, i converted the sequencer internals to a C- based octave. It helped. I also reworked the sequencing of the arpeggiator. Fixed a really boneheaded indexing problem caused by the fact that musical notation does not have a “zero.” I knew that, of course, but plum forgot to apply it to the apreggiator, as it ran through the chord intervals. For now, the fixes only work over the 15-interval (two octaves + one top tonic), so it’s not yet scalable for a wider range. I’m pretty sure I can come up with a more elegant solution that scales to an arbitrary number of octaves, but my brain is still cooling off from the latest flurry of activity.

I narrowed the fill pulse to 100 microseconds. Probably not a huge effect, although now the fill lights aren’t on long enough to see. I might up the pulse to 50ms or so later on.

Fixed various limit issues with the quantizer and scale query patches. Added a new output to the quantizer (which you’ll find in the new MIDI progression patch) that gives you the scale degree (as in i, ii, iii, iv, etc) you’ve hit, based on current key and scale.

The new midi progression patch now uses a quantizer to generate the degree of scale and octave hit, and because this requires knowledge of the current key, its output becomes key-neutral, which eliminates the need for the “-key” button on the sequencer.

The complete project’s chord tone patch board is set up to produce a straight 15-step arpeggio, beginning at the tonic and ending at tonic, two octaves up. Zero Hz freq from the midi at startup still defaults to C two octaves below A440. If you are in C-Major, you shouldn’t see any sharps or flats from the arpeggiator.

2 2 loop polyrhythm tone seq chord apregg v 9:10:18-1.audulus (2.4 MB)

[dcLargo]

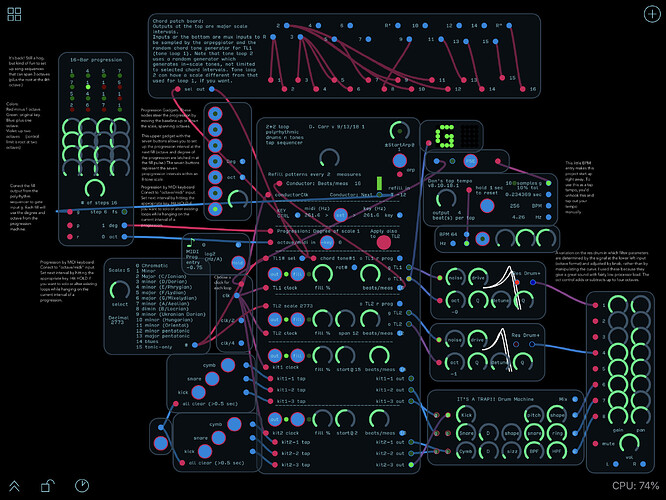
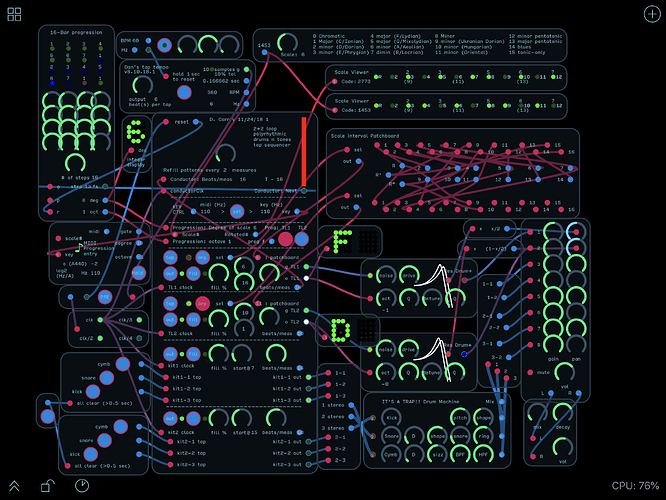
New one v9.18.18-1

2 2 loop polyrhythm tone seq chord apregg v 9.18.18-1.audulus (2.3 MB)

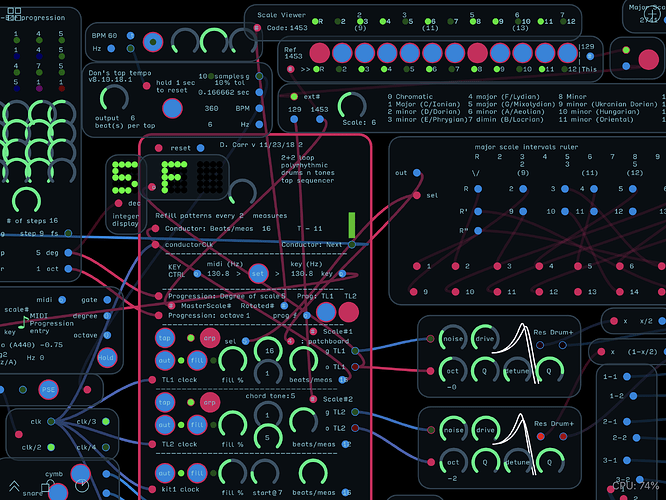
Switched to one scale for everything.

Important signal types:
I haven’t been totally consistent with signal naming in the project, but here are what I’d call the musically important signal types

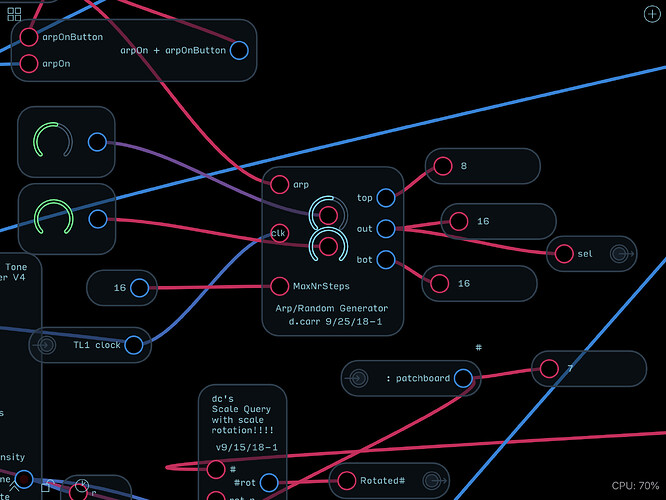
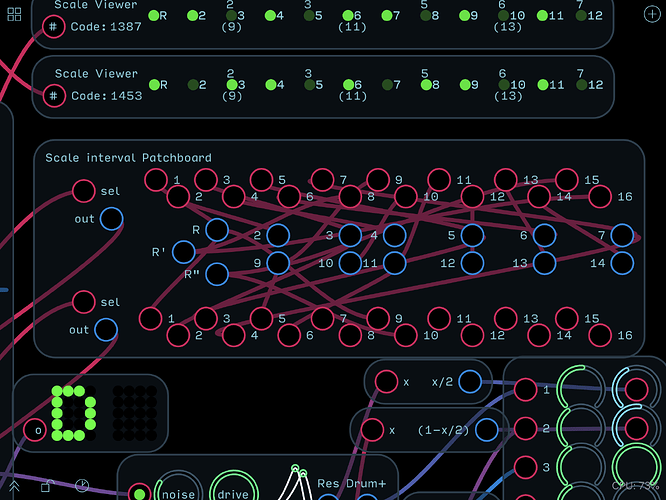
• Scale: integer (1 - 4095—Binary-derived) decimal code for various musical scales. The LSB is tonic, so scales will nearly always have an odd numbered code)
• Key: octave-format —the current key frequency
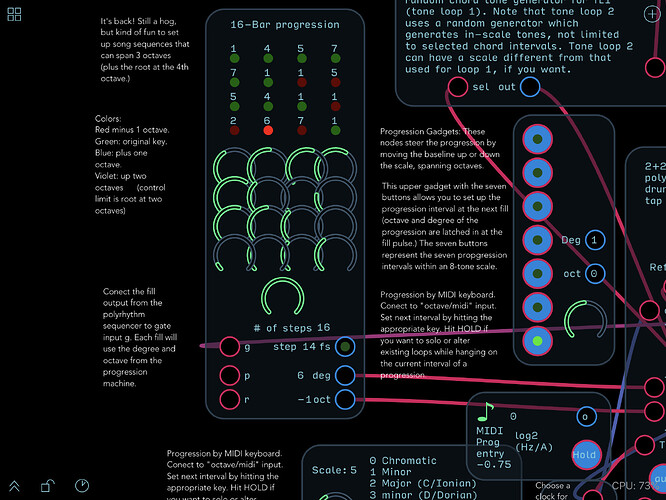
• Progression Octave: integer—, where 0 is original key octave
• Progression Degree: integer (1-7)—the current degree of scale of the progression
• Scale-rotated: integer (1 - 4095)— Scale code, bit-rotated to place the current progression degree of scale at position 1, allowing chords and arpeggios to remain in-scale (note that the code will always be an odd number if the scale is rotated correctly)
• Progression-interval: octave-format—root frequency of the progression, normalized to the current key.
• Melody interval: positive integer (1,2,3…)— in-scale tones, normalized to the current progression root.
• Melody octave: integer (…-2, -1, 0, 1, 2…)—number of octaves to the current melody tone.
• Melody interval: octave-format—melody, normalized to the current progression root.
• o TL out: octave-format—sum of key, progression octave, progression interval, melody octave, and melody interval.

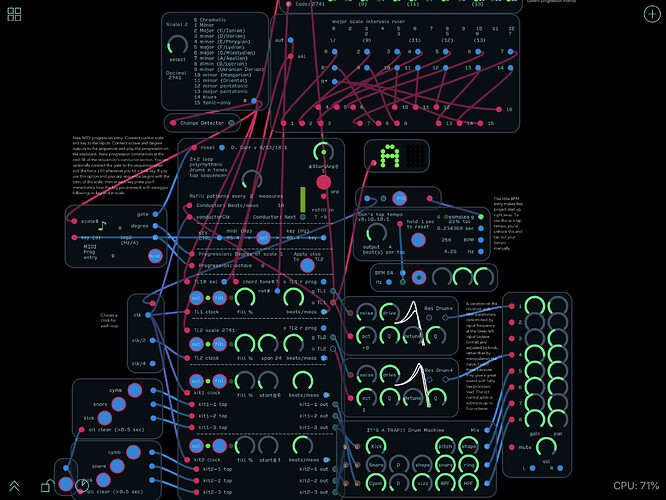
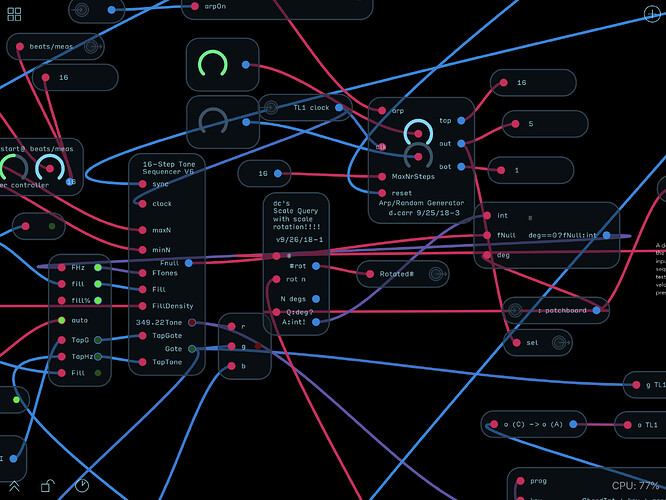
Added a “tap” button to the tone loops to allow you to tap out tones from midi if the loop is off-auto. Once you have a nice loop tapped out, you can run it over a progression.

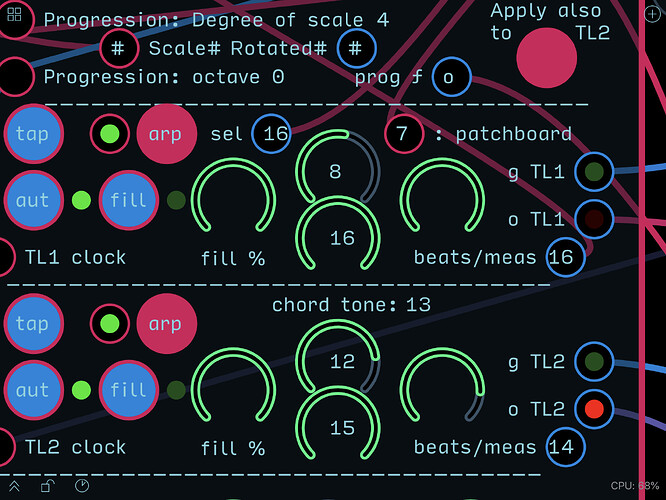
Tone loop 2 now randomly plays any in-scale tones over a two octave (plus 1 for high-tonic). You dial in the lowest tone you want and the highest (note, this is scale-based numbering, where 1 in a seven-tone scale represents the root, 8 is the root up one octave, and 15 is the root up two octaves.

Setting both dials in tone loop 2 to the same number forces the loop to just output that one tone. If you set the upper dial lower than the upper, You get the same tones as you’d get the other way, but inverted in order. For a random set of tones, direction has no meaning, but for arpeggios, in which you’d be actually outputting sequential indexes to the mux loaded with the tones, reversing the roles of the dials would reverse the arpeggio.
SO—I’m planning to add this two-dial approach to tone loop one, and probably make a single random/arpeggio patch to be used in both tone loops, were the chord tone patch board would be used by tone loop 1 and a straight sequence would be thre arp source for loop 2.

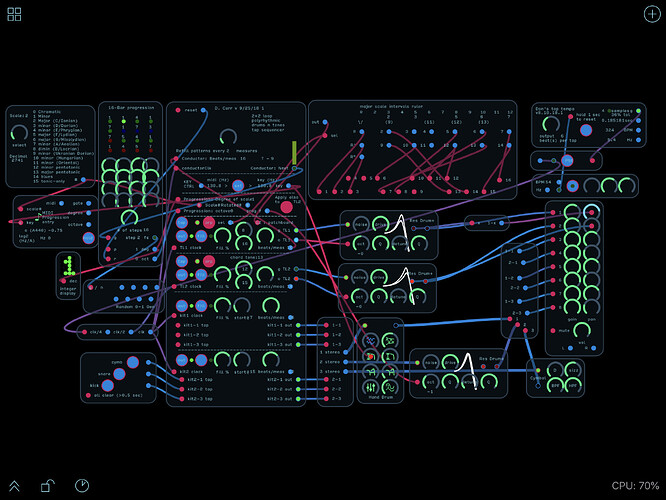
All octave signals outside of the sequencer UI are in Audulus A440 format, for compatibility with other folks’ patches.

Inversions: to do inversions (remember, this thing arpeggiates—it doesn’t do full-voiced chords) you just place the intervals where you want. Want to put the third below the root? You can, but that slides the rest of the chord up an octave. The problem with this at present is that my method of progressing up 1-7 intervals is via a brute-force if-then-else method which falls apart at two octaves. A better one’s coming! I swear! Some lovely, naturally terminating, recursive sort of expression for an arbitrary number of octaves is right on the tip of fingers! I’m certain this is reinventing the wheel. I believe, however, that reinventing the wheel is important if you want to learn more about wheels!

Will I be using any of this stuff in a year? Dunno, but it’s fun now, and still inspiring to listen to. Keeping everything in-scale may not help it sound more interesting, but I’ve figured that to develop an ear for a musical scale, you’d need to be exposed to it properly played. I hope I’m approaching that.

[robertsyrett]

This is crazy intricate. I love diving into the sub patching to see how it all ticks. Inspiring as always.

[dcLargo]

Latest, with a identical new bidirectional arpeggiator / random number generators on each tone loop. You set the start and and value on the knobs (lower knob is the start value) and the counter starts counting from start to end value. If you set the starting value higher than the ending number, a downward count results. Same value for stop or start just continues on that one value. Tone loop one uses the generator to select “sel” inputs to the patch board, so there are a maximum of 16 steps, corresponding to the 16 addresses for the patchboard. Tone loop two has its range interpreted as chord intervals, and is calculeted as follows: current scale’s tones par octave (calculated by the scale query patch) times number of octaves (currently 2), plus one to allow one tonic in the top octave.

2 2 loop polyrhythm tone seq chord apregg v 9.25.18-1.audulus (2.4 MB)

It’s connected to the progression generator again. Runs at about 60 % on my iPad Pro and at about 40% on my new old iMac (5 yo machine).

The new arpeggiator is kind of interesting in that you set the output range you want, and it scales the number of steps to fit in the 0-1 input range. This was done to allow simple switch from arpeggiator to random generator, allowing one little patch to do it all, instead of the kluge of using two hastily slapped together patches with fairly Byzantine signal/control routing.

Project:

Detail:

UI:

[dcLargo]

Added resets to the new arpeggiators. Forgot you need these things to restart at each progression change!

2 2 loop polyrhythm tone seq chord apregg v 9.25.18-3.audulus (2.5 MB)

[dcLargo]

Been meaning to to this: It occurred to me yesterday that since my arpeggiators now issue scale intervals, for which the numbering scheme is zero-free, I can now properly handle the “empty time slot on the chord tone patchboard” problem.

When a time slice on the patchboard (any selector from 1 to 16) is not patched to a scale degree, a value of zero appears at the appropriate time at the patchboard output. As there is no “degree zero,” this zero value is captured and converted to an octave signal which, while legal, is too extreme for any practical audio application.

2 2 loop polyrhythm tone seq chord apregg v 9.26.18-1.audulus (2.5 MB)

At the tone sequencer, before the octave signal is converted to Hz for storage in the loop, a test for that level is made. Any sample frequency meeting that criteria triggers a zero velocity value to be stored in the “gate” sequencer, effectively killing the tone loop output for that time slice.

The tone sequencers provide the value at the “Fnull” output, to allow encoding of the octave signal:

[dcLargo]

Another wrinkle: Allowing that sudden drop of 50 octaves — even without a gate pulse — seemed to give me a peek at the step response of my modified res drum pseudo-synths! So, I added an expr to the tone sequencers that swaps in zero as the frequency (octave format) for samples that contain the Fnull value (currently -50), rather than allowing it to pass on through.

2 2 loop polyrhythm tone seq chord apregg v 9.27.18-1.audulus (2.3 MB)

[justin.carper]

Beautiful monstrosity dc! I’m attempting to do something similar and learning a lot from your work.

[dcLargo]

I appreciate the nod! God speed, Justin Carper!

[dcLargo]

Small change: I wanted to try running one loop with a partial version of the main selected scale without rewiring scales on the fly, so I gave the scale selector thing two outputs, with the new output issuing the code for the alternate scale, based on the state of input “Alt#.” With “Alt#” disconnected or at zero, both scale outputs give the full scale. The button bar still has the reference lights and interval ruler, and in the present setup the primary selected scale is used as the reference, so you can use only intervals that are in scale if you want.

Another change: You can apply the progression to either loop. Note the two buttons in the progression section, below the KEY CTRL section.

In the sequencer behemoth, I’ve added separate scale inputs for the progression input section (MasterScale#, just beneath the KEY CTRL section) and for the two tone loops (Scale#1 and Scale#2). A scale code is normally always applied to MasterScale# (a code of zero at MasterScale# results in the default 12-tone chromatic scale—code 4095, if that’s your thing!). If a tone loop’s scale input is left open (or is set to zero), then the scale applied at MasterScale# is used for that loop.

Refresher on the sequencer tone loops — The tone loops either arpeggiate or issue values at random. For tone loop 1, the values (from one to 16, or a subset) are interpreted in this project as time slices for the patchboard, where you hard-wire intervals (notes) over a two octave range (plus one high root). This allows custom loops to be made and changed on the fly. (A patchboard that’s left open results in a rest for that time slice.)

The values for loop 2 correspond to the available intervals on whatever scale is being used, over the same “two octave + one root” range. The math for that is done using the Ndegs (as in “number of degrees”) output from the loop 2 quantizer, times 2 for the number of octaves, plus 1 for the root of the third octave. In the case of a partial scale applied to Scale#2 containing only a root and a fifth, you’d get five available values to play.

Another tiny change to the scale selector—I rearranged the scales to allow scale number 1 to be the major scale, with its six additional modes following in their traditional numbering order.

2 2 loop polyrhythm tone seq chord apregg v 11.23.18-2.audulus (2.7 MB)

[dcLargo]

Change of heart. The experiment with two scales led to too many problems—mainly overall complexity and the ability to keep progressions in-scale (not to say it’s a crime to step out of scale. It’s just not my goal with this project).
SO, I’ve decided to make loop 2 a copy of loop 1, with an additional patchboard mux for it.

2 2 loop polyrhythm tone seq chord apregg v 11.24.18-2.audulus (2.7 MB)

Now, both tone loop sequencers can access from 1 to 16 time slices. As before, you can set the starting slice (bottom knob) and ending slice (top knob), and you can set the loop to play in reverse (top slice < bottom slice) or to hold on just one note (top slice = bottom slice). Leaving a time slice open results in a rest for that time slice, as before.

Tone looper button/knob review:

• Aut — Refill loop automatically
  —ON == Auto refill the loop each step in a progression (in other words, when the Conductor’s “baton” flashes green!)
  —OFF == Do not refill. Leave the loop intact. A tap of the fill button clears the loop. Accept MIDI input (if Tap is ON, below)
• Fill — force a fill/reset right now. This will take one pass through the loop to complete, and only over the range set by the range knobs.
• Arp — ON == Arpeggiate over the step range set by the dials.
  — OFF == Play the steps randomly over that same range.
• Range Knobs — Set range and direction over which the looper is to play, record, or clear tones. Bottom knob sets the first step and the top knob sets last step.
• Fill % — With Aut(o) ON, this sets the probability a sample will be recorded on an auto-fill, from 0 to 100%. With Aut(o) OFF, the value is set to zero (clear), regardless the setting of the knob.
• Tap — ON == Accept inputs from MIDI (If the conductor is set to loop more than once, then notes are saved only if played during thre first pass through the loop)

I reworked the UI of the patchboard to assist in visualizing the time slices when patching patterns. You map any of the 15 chord intervals (2 octaves + the root of the third octave) to one or more of the 16 time steps.
An empty time step is a rest. Pretty straightforward.

11/28 addition:
I tried out that “Curved Synth” with the monster (with an envelope output added). I backed off the fill density of tone loop 1 to allow that synth to go wacky here and there. It’s playing through a custom scale (buttons). Kind of sounds like R2D2!

2 2 loop polyrhythm tone seq chord apregg v 11.28.18-1.audulus (2.7 MB)

[futureaztec]

This is great. Thanks for all that work.