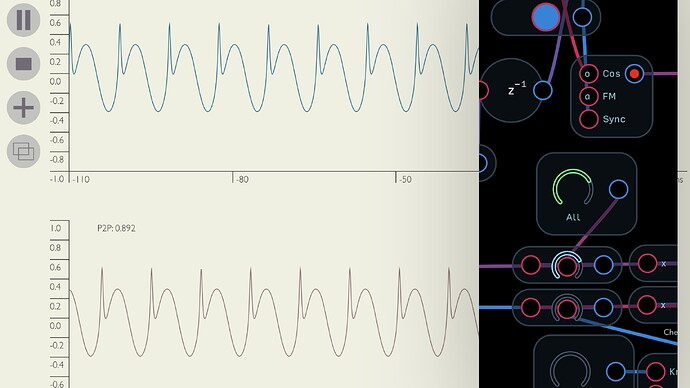
After having taken a look at the Rob Hordijk Masterclass given at Sines & Squares 2014, I was inspired to take another look at using the Fourier sine/cosine combination waveform in conjunction with correcting the linear feedback in Hordijk’s Harmonic Oscillator.
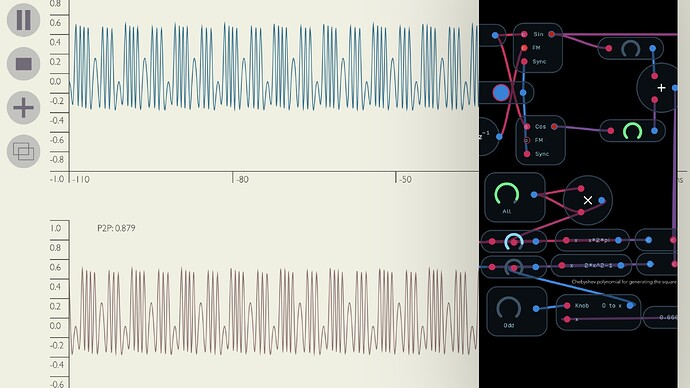
This time round I have gotten it to work somewhat. The linear FM from the combined sin/cos signal is only applied to the sine oscillator, and the resulting wave is much richer than was possible with phase modulation. There is however a small but important detail – while the level for the sine feedback appears to be fully turned up, it is in fact very slightly reduced. This, for some reason, is what enables the result. When turned up fully the addition of harmonics by turning up the Linear FM and All/Odd knobs breaks down at certain points. (These breaks are quite interesting in themselves, especially at lower frequencies – something that could be explored further as a feature in itself.) A similar effect can be achieved by detuning one of the oscillators very slightly – something I discovered by accident, but which is the detail that gets the thing to work at all.
The waveform also gains much of it brightness from an extra spike, rather than approaching a sawtooth.
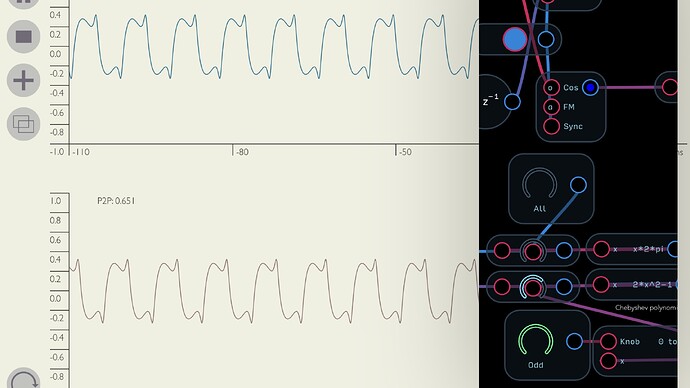
The odd harmonic feedback using the Chebyshev polynomial also allows for a slightly richer wave than was possible with phase modulation, but combining the all and odd waves unfortunately causes the feedback to break down completely.
Alternatively if the sine feedback is turned down completely one can achieve much cleaner FM timbres and the odd and all harmonics can be happily combined, even though the odd harmonics are much more easily drowned out.
These experiments haven’t brought me closer to recreating Hordijk’s Harmonic Oscillator, but have been interesting nonetheless.
Sin Cos OSC HRM.audulus (37.5 KB)